You may have heard about NumPy and wondered why it seems so essential to data analysis in Python. What makes NumPy seemingly end up everywhere in statistical calculations with Python? Here are some good reasons.
NumPy Makes It Easy to Create Multidimensional Arrays
Science and engineering, including statistics and data science, rely heavily on linear algebra, which will be mentioned later. Representing vectors and matrices means that developers need an easy way to implement and access multidimensional numerical arrays.
Without a library, this would require a significant amount of tedious programming and iteration using loops, which can be cumbersome to manage and slow down the system, especially with an interpreted language like Python. As with other Python libraries, the job has largely been done with NumPy.
You can create a 1-dimensional array like this:
import numpy as np
a = np.array([1,2,3,4])
This is similar to standard Python arrays, with the elements enclosed in square brackets. In NumPy parlance, this array has one axis. It could represent simply a list of numbers, or it could be a vector. This would be similar to a vector in R, another language popular in statistics and data science.
You can also create arrays from sequences using the arange function. For example, to create an array of even numbers between 2 and 8:
np.arange(2,10,2)
The first number is the lower bound, the second is the upper bound, and the last is the step size, which means that NumPy will count by 2.
You can also use the arange function for floating-point numbers:
np.arange(2,10,2)
np.linspace(0,50,100)
This will create an evenly spaced array of 100 numbers between 0 and 50.
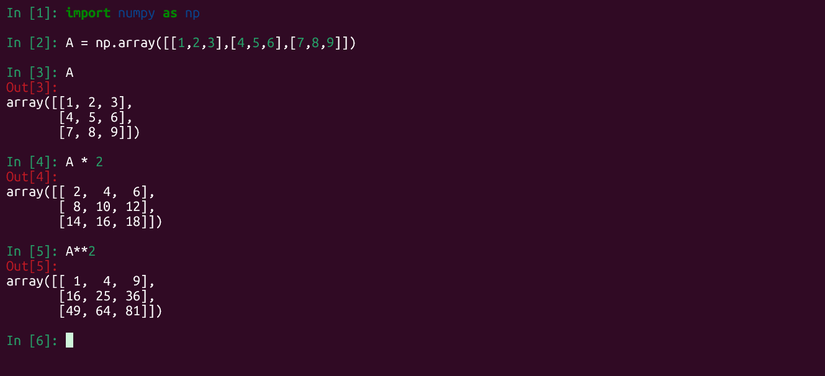
You can also create a two-dimensional array that could represent a matrix. You could create an array that’s three rows by three columns and then examine it in an interactive session, such as in IPython or a Jupyter notebook:
A = np.array([[1,2,3],[4,5,6],[7,8,9]])
AEach row of the array is enclosed in square brackets. It’s effectively an array of arrays. In matrix terms, since both the number of rows and columns in this array are equal, this would be called a “square matrix” in linear algebra. It’s easy to translate mathematical ideas into these arrays, which is why Python is becoming a language of choice in data science and analysis.
Fast Numerical Computation
NumPy is known for its speed in calculations. You might not notice this with smaller operations on a PC, but on bigger systems doing lots of calculations performance matters. While Python is known as an interpreted language, NumPy internally uses C and Fortran code, including the LAPACK and BLAS libraries, to give numerical calculations a speed boost.
C and Fortran have been used in scientific computing for many years, and the numerical computing libraries they rely on have been carefully tuned to wring the best performance out of the silicon they run on. Building on this legacy of fast computation, NumPy drastically speeds up the statistical operations of modern data science and analysis.
Easy Basic Stats Calculations
One reason Python and NumPy are so popular in stats applications is that it’s easy to perform a lot of the standard basic descriptive stats calculations on arrays. The Python built-in statistics module does have these, but it’s intended for simple operations you’d peform on a hand calculator rather that wouldn’t scale to larger NumPy arrays.
NumPy arrays have a lot of built-in “universal functions” you can perform. A good example is the mean, or average, which is just the sum of all the data points divided by their number.
To get the mean of the array we defined earlier:
a.mean()
This also works for the square matrix we also created.
A.mean()
You can also take the median, or the middle value of the data:
np.median(a)
You can also take the standard deviation
a.std()
These simple operations and others are why NumPy is a building block for statistical analysis with Python.
Random Numbers
NumPy also makes it easy to generate randrom numbers. This is important in statistics and probability because it lets you generate test data quickly.
To generate random numbers, you have to define a random number generator, or rng object:
rng = rng = np.random.default_rng()
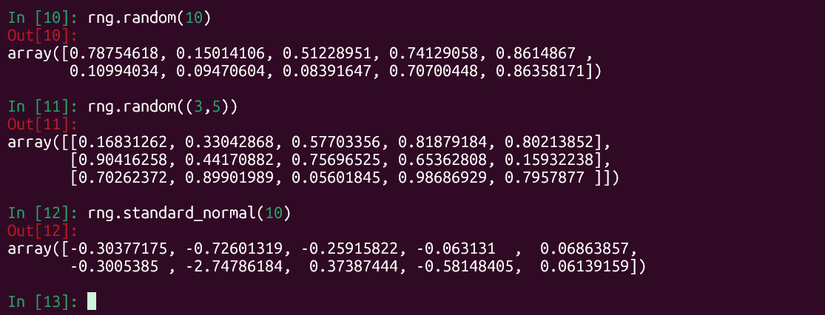
To create an array of random numbers, you can just use the random function on the new rng object:
rng.random(5)
This will create a list of five random numbers.
You can also draw random numbers from specific probability distributions. To get random numbers from the normal distribution, with the famous bell-shaped curve, use the standard_normal function
rng.standard_normal(5)
You can also create multi-dimensional arrays. For example, to create a 3×5 array of random numbers:
rng.random((3,5))
Easy Access to Common Constants
Another feature that makes NumPy popular for statistical analysis is that it includes popular constants like pi and e. While you can access these in Python’s math library, NumPy’s versions are more suitable for using with large arrays.
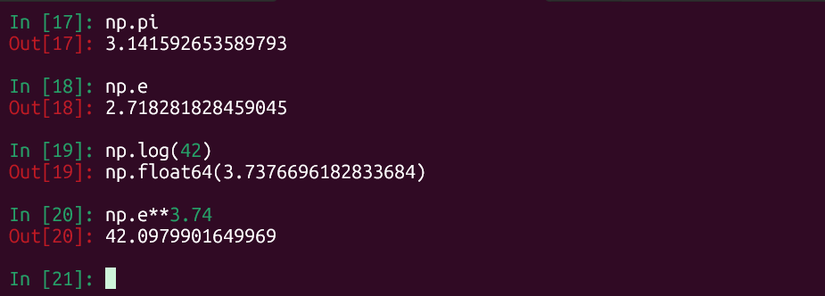
To get an approximation of pi:
np.pi
And of e:
np.e
You can use them in calculations. The natural logarithm, with the base e,is one of the universal functions mentioned earlier. Let’s take the natural logarithm of 42:
np.log(42)
The answer is approximately 3.74. We can get back to our original value by using raising e to the power of the logarithm:
np.e**3.74
Since e is widely used in business and finance to model exponential growth, it’s useful in a lot of real-world contexts. This is why NumPy has found a lot of applications in turn.
Linear Algebra
As mentioned earlier, linear algebra is ubiquituous in the scientific world, and that includes statistics. The main reason is that it takes the systems of linear equations you might have learned about in a high school algebra class and represents them in a more compact form, without all those annoying letters. With the speed of numerical computation that NumPy offers, it makes solving the kind of equations that come up in statistics much easier and faster than doing things by hand.
The most obvious application of linear algebra in statistics is in linear regression, where you fit a line over a bunch of data points to minimize the square of the distance to the scatterplot of data. When you have data points numbering in the hundreds and possibly thousands, not even the biggest math nerd is going to try to attempt to solve a system by hand. It’s better to use NumPy to do this instead and save the labor of a researcher instead. NumPy makes it easy to get answers quickly to statistical questions.
Other Libraries Depend on It
Most of the time, you aren’t using NumPy by itself. Because NumPy is so widely accepted in the scientific Python ecosystem, a lot of libraries will use it behind the scenes. The pandas library will arrange your data into spreadsheet-like DataFrames. Seaborn will create plots of your data. You can run regression analyses and statistical tests in statsmodels, pingoun, and SciPy’s stats module. SciPy itself is a companion library to NumPy, offering all kinds of operations, including probability distributions, information on the skew of a dataset, and others. Scikit-learn also offers advanced machine-learning capabilities. All of these work on top of NumPy data and extend its capabilities.
With all of these libraries, Python offers a more flexible alternative to monolithic programs like Wolfram’s Mathematica. It’s more powerful than Excel, and needs fewer clicks. Since Python is already a popular scripting language, it’s also easy to write scripts to automate repetitive operations. The Jupyter notebook came out of this scienitific community, and it offers a way to share repeatable results. Reproducibility is important in science. Other researchers need to be able to duplicate your work to verify it.
For all these reasons, Python is becoming a language of choice for statistics.